2018- Centres étrangers 2
1.1 La chronophotographie montre que la poignée parcourt une même distance d pendant une même durée t. La vitesse $v = \frac d t$ est donc constante.
1.2. Le mouvement est rectiligne uniforme :
- rectiligne car la trajectoire est une droite
- uniforme car la vitesse est constante
2.1. L'atome dont le numéro atomique est 3 est le lithium. Son symbole est Li.
2.2.
Modèle 1 : il manque 1 charge négative (portée par un électron) pour que l'atome soit neutre.
Modèle 2 : les charges - sont normalement autour du noyau qui, lui, porte des charges positives. Là c'est le contraire.
Modèle 3 : il est correct car l'ensemble est neutre et les charges sont placées au bon endroit.
2.3.
1 : chimique
2 : électrique
2.4. Sous forme d'énergie thermique.
3.1.1.
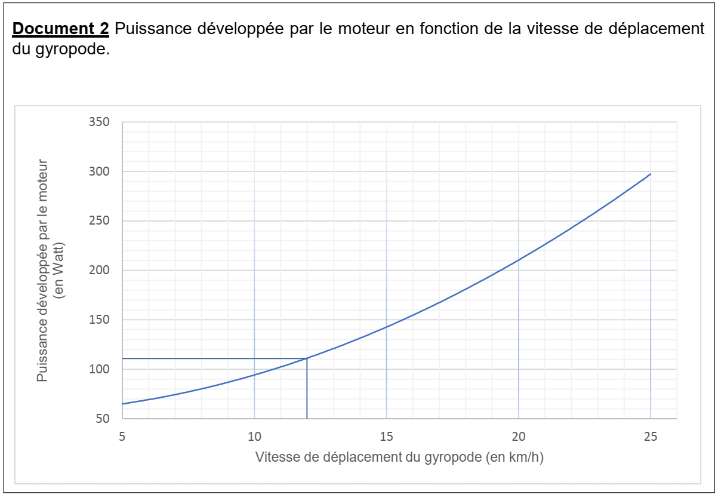
On lit P = 110W pour v = 12km/h
3.1.2. $E = P \times t$
3.1.3. Calculons l'énergie consommée par le gyropode pendant 6h.
$E = P \times t$
E en Wh
P en Watt (W) : P = 110W
t en heure (h) : t = 6h
$E = 110 \times 6 = 660Wh$
La batterie pouvant fournir une énergie de 680Wh, on peut utiliser le gyropode pendant 6h à 12km/h
Pour répondre à cette question, on peut aussi calculer la durée :
$t = \frac E P = \frac {680} {110} = 6,18 h$
On peut donc rouler plus que 6h.
Il est préférable de répondre avec la 2ème méthode car la question suivante nous demande de calculer la distance parcourue.
3.1.4.
En 6,18h et en roulant à 12km/h, on peut parcourir la distance :
$d = v \times t = 12 \times 6,18 = 74.2km$
3.2.
A 24km/h, la puissance est de P = 280W
Avec la batterie de 680Wh, on peut rouler pendant :
$t = \frac E P = \frac {680} {280} = 2,43 h$
En 2,43h et en roulant à 24km/h, on peut parcourir la distance :
$d = v \times t = 24 \times 2,43 = 58,3km$