Semaine du 6/12/21
0. Correction du DS
1 Correction du travail à faire
Activité p 66 67
1. Le Soleil attire les planètes. La Terre attire la Lune.
2. La Lune attire la Terre.
3. La Terre attire la Lune et réciproquement donc il y a interaction.
Idem pour le Soleil et la Lune.
4. Interaction attractive à distance.
5. Cette interaction concerne tout ce qui a une masse.
6. La gravitation est une interaction attractive à distance qui concerne tous les objets ayant un masse.
2. Leçon à écrire côté leçon
:3eme:2021-12-10chapitreivgravitationuniverselleetevolutiondeluniverslecon-eleves.pdf
Chapitre IV : Gravitation universelle et évolution de l'Univers
I. Qu'est-ce que la gravitation universelle ?
La gravitation est une interaction attractive entre deux objets qui ont une masse. C'est une interaction à distance qui dépend de la distance qui sépare les deux objets.
La gravitation gouverne tout l’Univers (système solaire, étoiles, galaxies et pommes).
II. Les forces de gravitation
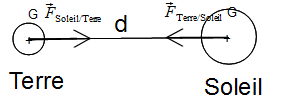
La gravitation qui s'exerce entre 2 objets A et B peut être modélisée par deux forces ${\vec F}_{A/B}$ et ${\vec F}_{B/A}$ :
- de même direction
- de même valeur
- de sens opposé.
- de valeur
$F_{A/B} = F_{B/A} = G \times \frac {m_A \times m_B} {d^2}$
$m_A$ : masse de l'objet A
$m_B$ : masse de l'objet B
$d$ : distance séparant les centres de gravité des 2 objets
$G$ : constante de gravitation $6,67 \times 10^{-11} N.m^2.kg^{-2}$
(formule à ne pas connaître par coeur mais à savoir utiliser)
3. Exercices à commencer à en classe et à finir pour la prochaine fois
Exercice calculatoire
Calculer la force exercée par la Terre sur le Soleil.
Calculer la force exercée par la Terre sur la Lune.
Calculer la force exercée par la Terre sur votre trousse de 200g.
Calculer la force exercée par un stylo sur un autre espacé de 10cm.
Masse du Soleil : mS = 2,0 × 1030 kg
Masse de la Terre : mT = 6,0 × 1024 kg
Masse de la Lune : mL = 7,342 × 1022 kg
Distance Terre-Soleil : d = 150 × 106 km
Distance Terre-Lune : d = 384 000 km
Rayon de la Terre : RT = 6400 km
Loi de gravitation universelle :
$F = G \times \frac {m_A \times m_B} {d^2}$ avec G = 6,67 × 10-11 N.m2 .kg-2 , d en m, mA et mB en kg
Exercice 10 p 77
Exercice 11 p 77
Exercice 12 p 77
Exercice 16 p 77
4. Facultatif (pour les costauds)
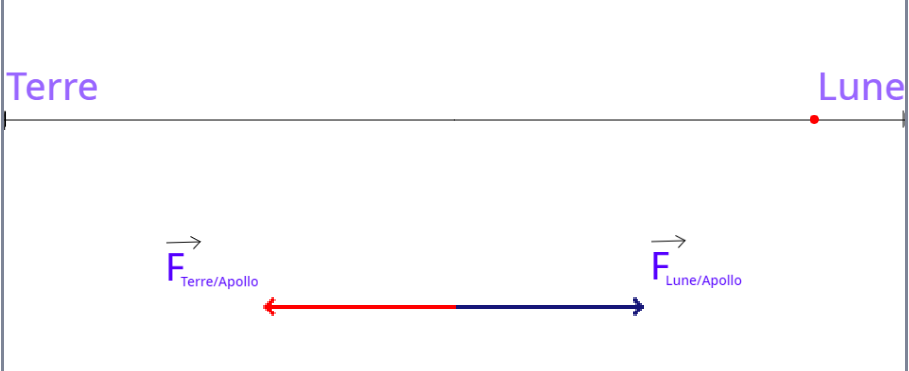
Distance Terre Lune dTL = 384 400 km
Masse du module lunaire Apollo mA = 1,5 × 104 kg
Masse de la Terre : mT = 6,0 × 1024 kg
Masse de la Lune : mL = 7,342 × 1022 kg
A quelle distance du centre de la Terre le module Apollo est-il autant attiré par la Lune que par la Terre ?
Il est possible de résoudre le problème de façon précise en résolvant des équations mathématiques. Il est plus simple de résoudre le problème en utilisant un tableur ou en programmant dans scratch.