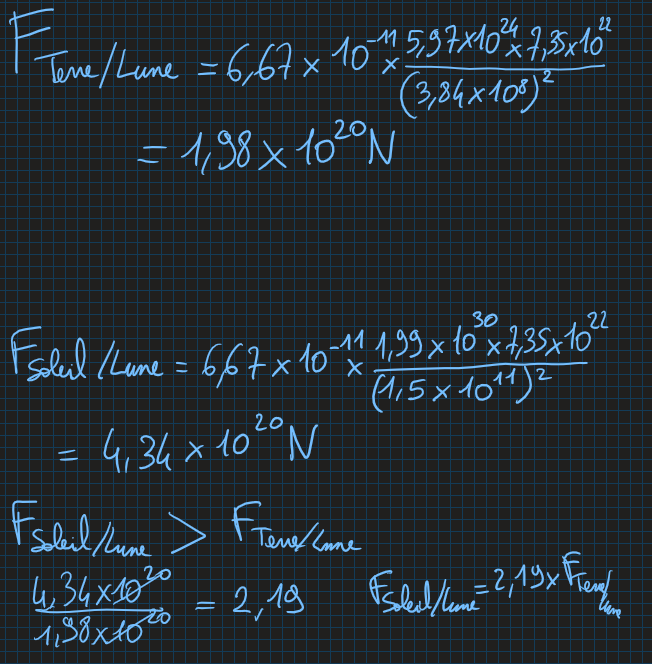Ceci est une ancienne révision du document !
Côté exercice
Exercices calculatoires.
- Calculer la force exercée par la Terre sur le Soleil.
- Calculer la force exercée par la Terre sur la Lune.
- Calculer la force exercée par la Terre sur votre trousse. On prend une masse de 200g pour la trousse. Il faut bien penser à convertir en kg.
- Calculer la force exercée par un stylo sur un autre espacé de 10cm. On prend une masse de 5g pour la trousse. Il faut bien penser à convertir en kg.
| Masse du Soleil : mS = 2,0 × 1030 kg | Masse de la Lune : mL = 7,342 × 1022 kg | Distance Terre-Lune : d = 3 84 000 km |
| Masse de la Terre : mT = 6,0 × 1024 kg | Distance Terre-Soleil : d = 150 × 106 km | R ayon de la Terre : R T = 6400 km |
Correction
Exercices calculatoires.
Calculer la force exercée par la Terre sur le Soleil.
C'est la même valeur que la force exercée par le Soleil sur la Terre.
$F = G \frac {m_A \times m_B} {d^2} = 6,67 \times 10^{-11} \times \frac {6,0 \times 10^{24} \times 2,0 \times 10^{30}} {(150 \times 10^9)^2} = 3,6 \times 10^{22} N$
Calculer la force exercée par la Terre sur la Lune.
$F = G \frac {m_A \times m_B} {d^2} = 6,67 \times 10^{-11} \times \frac {6,0 \times 10^{24} \times 7,342 \times 10^{22}} {384000000^2} = 2,0 \times 10^{20} N$
Calculer la force exercée par la Terre sur votre trousse.
mtrousse = 200g = 0,2 kg
$F = G \frac {m_A \times m_B} {d^2} = 6,67 \times 10^{-11} \times \frac {6,0 \times 10^{24} \times 0,2} {(6400000)^2} = 2 N$
Calculer la force exercée par un stylo sur un autre espacé de 10cm.
mstylo = 5g = 0,005 kg
$F = G \frac {m_A \times m_B} {d^2} = 6,67 \times 10^{-11} \times \frac {0,005 \times 0,005} {(0,1)^2} = 1,7 \times 10^{-13} N$
Cette force est extrêmement faible.
Exercice 10 p 77
Exercice 11 p 77
Exercice 8 p 90
Exercice 11 p 91
a. P = 3,2N
b. $m = \frac P g$
P en N
g en N/kg
m en kg
$m = \frac {3,2} {9,8} = 0,33~kg = 330~g~environ$
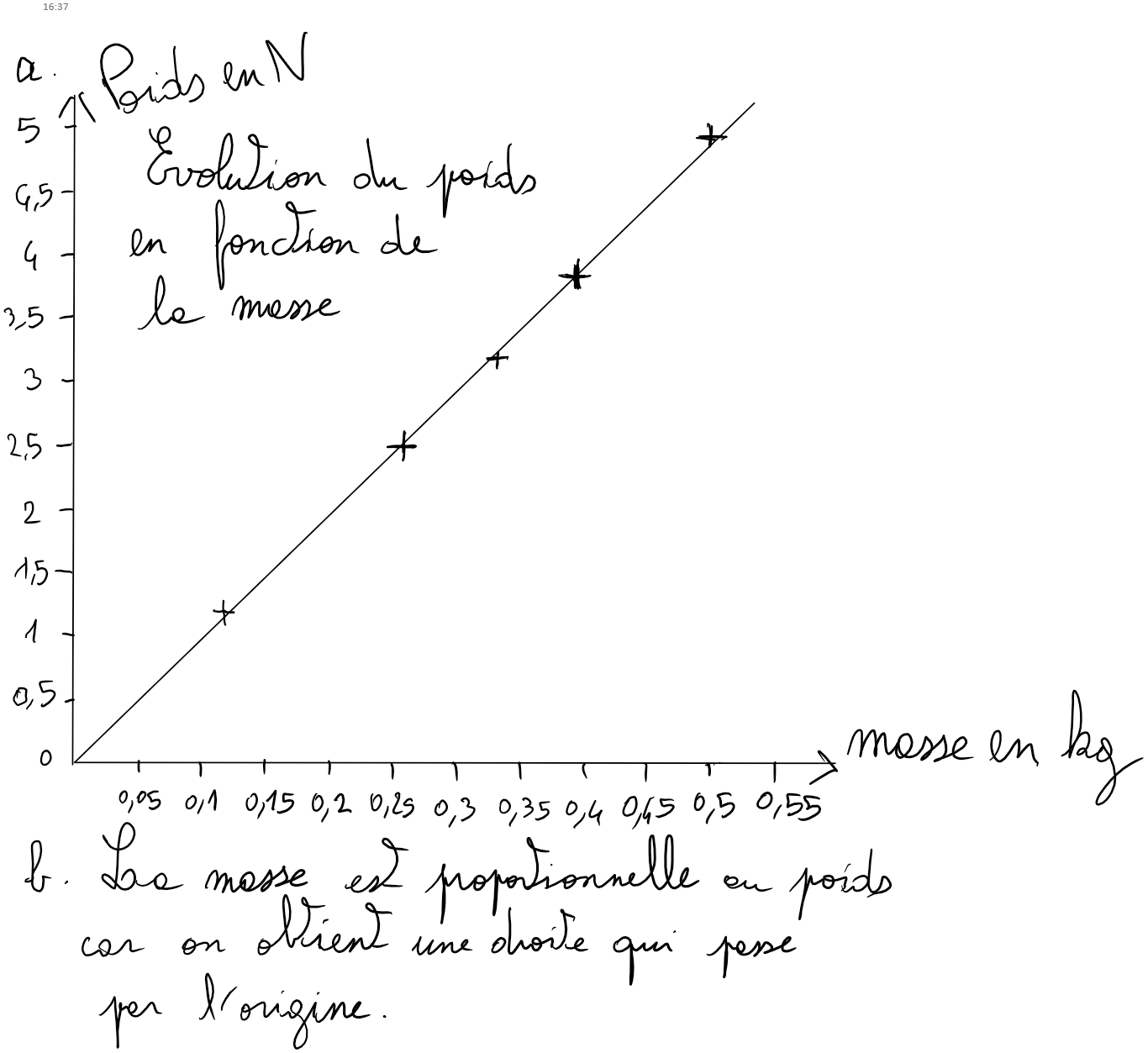
Exercice 13 p 91
$g = \frac P m$
P en N
m en kg
g en N/kg
$g = \frac {9990} {900} = 11,1 N/kg$